Research Vignette: Generalization and Interpolation
by Daniel Hsu
 The practice of deep learning has attracted new attention to several basic questions in statistical machine learning. One such question is how fitting machine learning models to relatively small “training” data sets can lead to accurate predictions on new data. In machine learning jargon, this is the question of generalization.
The practice of deep learning has attracted new attention to several basic questions in statistical machine learning. One such question is how fitting machine learning models to relatively small “training” data sets can lead to accurate predictions on new data. In machine learning jargon, this is the question of generalization.
The conventional wisdom in machine learning offers the following about generalization:
- A model that is too simple will underfit the true patterns in the training data, and thus, it will predict poorly on new data.
- A model that is too complicated will overfit spurious patterns in the training data; such a model will also predict poorly on new data.
Consequently, one should choose a model that balances these concerns of underfitting and overfitting [30]. A textbook corollary is that a model that exactly fits — i.e., interpolates — the training data “is overfit to the training data and will typically generalize poorly” [17].
Recent machine learning practice appears to eschew this conventional wisdom in a dramatic fashion. For instance, a common starting point for training a neural network is to find a model that exactly fits the training data [27]. (Typically, the model is subsequently fine-tuned using different criteria, but the starting point is already nontrivial.) While this may be difficult or impossible with small neural networks, it becomes substantially easier after making the network very large. It is remarkable that this practice is compatible with generalization, despite the concerns about overfitting.
This apparent contradiction of conventional wisdom is not new. In the last century, machine learning practitioners were already aware of the efficacy (and advantages) of using “oversized” neural networks where the number of model parameters exceeds the number of training data [9, 20]. Similar observations were made about large ensembles of decision trees: it was found that increasing the number of decision trees in an ensemble could improve accuracy, even beyond the point at which the ensemble exactly fit the training data [28]. These empirical observations motivated the development of a new theory that greatly sharpens the existing body of knowledge in statistical machine learning [1, 28], and this theory has been recently extended to deep neural networks [2, 15, 26].

However, the new theory does not fully explain recent observations about interpolating neural networks. First, in more recent experiments, neural networks are trained to interpolate noisy data [34]. By noisy data, we mean data in which the prediction targets (labels) may be erroneous. In fact, experiments have been conducted in which noise is deliberately injected in the data by assigning random labels to subsets of the training data. Neural networks that interpolate these data were nevertheless found to have nontrivial accuracy on new data. Second, similar phenomena have been observed in the context of predicting real numerical targets. (The aforementioned theoretical and empirical studies mostly focused on classification targets.) When predicting real numbers, it is almost always a given that training data will have noisy labels, so the thought of interpolating training data seems even more preposterous. But again, in recent experimental studies, interpolating (or nearly interpolating) models were found to have nontrivially accurate predictions on new data [4, 7].
Spurred by these recent empirical observations, researchers, including several participants of the Foundations of Deep Learning program at the Simons Institute, have begun to investigate statistical properties of interpolating models. While the observed phenomena are not yet well understood in the context of neural networks, there has been substantial progress toward understanding interpolation with related types of models, namely local prediction models and linear regression models.
Local prediction models are among the most well-known nonparametric methods used in machine learning, as they include prediction models such as k-nearest neighbors and kernel smoothers. However, such methods are rarely used to form interpolating models, as they are usually tuned to explicitly balance bias and variance (which is analogous to balancing underfitting and overfitting). One exception is the well-known special case of 1-nearest neighbors, which does yield an interpolating model since the closest example to a training example is itself (assuming no ties) [11, 13]. Another exception is the Hilbert kernel regression estimate [12] (also known as Shepard’s method [29]), which is an instance of a Nadaraya-Watson kernel smoother [24, 31]. This method uses a kernel function with a pole at zero, so its prediction at any training example is the label associated with that example (again, assuming no ties). Although each of these interpolating models has some drawbacks, it was recently demonstrated that they can be overcome with careful localization [5]:
-
For binary classification, the asymptotic error rate of 1-nearest neighbor is roughly twice the optimal error rate [11]. In some sense, 1-nearest neighbor localizes too much. If predictions instead come from piecewise linear interpolations based on multivariate Delaunay triangulations — which are, incidentally, dual to the Voronoi tessellations used by 1-nearest neighbors — then under certain distributional conditions, one obtains an improved asymptotic error rate in high dimensions: roughly 1 + 2 − Ω(d) times the optimal error rate in d-dimensional Euclidean space [5]. (A similar improvement is also obtained for regression.)
-
The Hilbert kernel regression estimate is statistically consistent (for both classification and regression), but it has no non-asymptotic rates of convergence [12]. It seems that this method does not localize enough. By instead localizing the smoothing with the same kernel function — e.g., to the k-nearest neighbors rather than all training examples — it is possible to obtain non-asymptotic rates of convergence. When k is appropriately chosen, the convergence rate becomes minimax optimal for Hölder smooth target functions [5, 8].
Although local prediction models seem rather different from neural networks, they in fact share many common features. For instance, neural networks are often used with many more parameters than training examples, so they can be regarded as nonparametric methods, like local prediction models, rather than parametric methods. Moreover, there is empirical evidence that large neural networks share a “local elasticity” property also possessed by other nonparametric methods, like nearest neighbors [18].
Linear regression models are also highly related to neural networks. After all, a feedforward neural network can be regarded as a linear regression model over a nonlinear feature map. Of course, the catch is that the parameters of the feature map are typically tuned alongside the linear regression coefficients. Certain linearizations of neural networks are related to neural networks in some training regimes [10, 19], but the relevance of these linearizations for understanding fully trained neural networks is debatable [14, 33]. In any case, understanding interpolating linear regression models is a natural first step toward understanding interpolating neural networks and is of interest in its own right.
When a linear regression model is made to interpolate training data, there can generally be infinitely many such interpolations: this is the underdetermined setting of the classical least squares problem. A particular fit that has received considerable attention is the least Euclidean norm fit, which is always uniquely determined. When the random covariate vector and label are jointly Gaussian, the prediction risk of this method has been fully characterized, up to constant factors, in terms of the eigenspectrum of the data covariance [3]. From this characterization, one can read off conditions on the eigenspectrum under which the risk goes to zero with the sample size. Similar conditions can also be obtained under other feature designs and intuitively explained in terms of signal “aliasing” [23]. Finally, the risk can also be characterized under high-dimensional asymptotics, where the data dimension d grows linearly with the number of training data n; these analyses can also be extended to certain nonlinear feature maps related to kernel machines and neural network linearizations [16, 21, 22].
Another natural question about linear regression models is whether explicit “capacity control” should be used. In particular, when the number of available features N greatly exceeds the number of training data n, then how many features p ∈ [0, N] should be used in the fitted linear regression model? Of course, if there are only a few relevant features, then naturally it would be advantageous to just select those if possible. However, when there are many relevant features but each is individually only weakly predictive, then the advantage of feature selection becomes less apparent. This latter scenario appears to be commonplace in many machine learning setups. Under various random designs with this “weak features” assumption, one can characterize conditions (on the covariance eigenspectrum, similar to [3]) in which every non-interpolating model with p < n features is strictly dominated by the least Euclidean norm interpolator (with p = N features) in terms of predictive risk [6, 32]. As above, these analyses can be extended to some nonlinear feature maps [22].
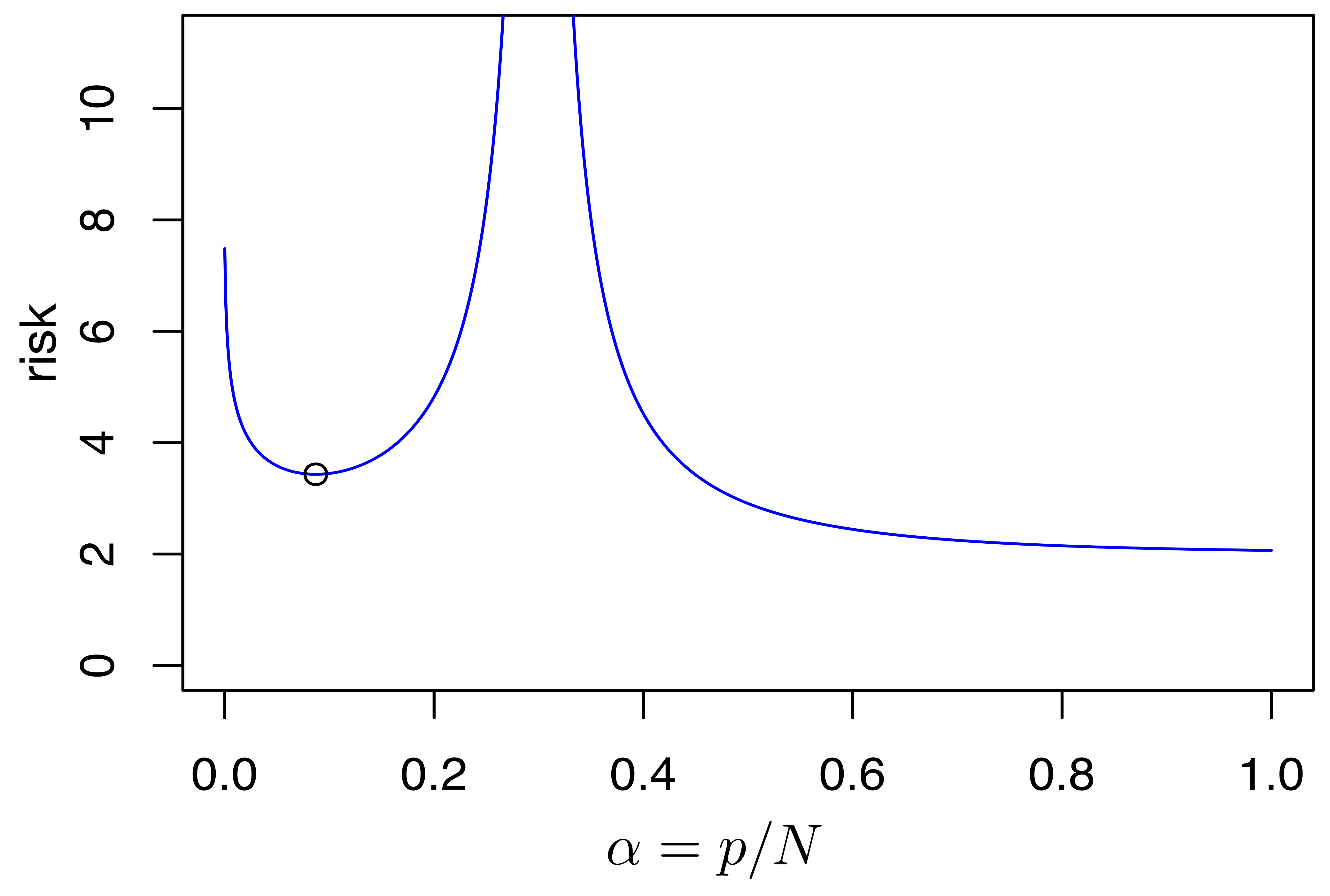
Figure 2: Plot of the asymptotic risk of linear regression models fit using either ordinary least squares (p < n) or least Euclidean norm interpolation (p ≥ n) under the “weak features” assumption (reproduced from [32]). The high-dimensional asymptotic limit has p/N → α and n/N → β = 0.3. The Gaussian design has a covariance matrix with eigenvalues decaying as λj ∝ 1/j. The black circle marks the local minimum in the range α < β (where p < n); this point is higher than the risk at α = 1 (where p = N).
These new analyses for local prediction models and linear regression models demystify the compatibility of generalization and interpolation, and they provide a counterpoint to the conventional wisdom about overfitting. Of course, there is still much to be done to understand generalization with neural networks as used in practice, especially as new mysteries continue to be uncovered (e.g., [25]). However, important initial steps have now been taken, and the Foundations of Deep Learning program has been instrumental in this research.
References
[1] P. L. Bartlett, “The sample complexity of pattern classification with neural networks: The size of the weights is more important than the size of the network,” IEEE Transactions on Information Theory, vol. 44, no. 2, pp. 525–536, 1998.
[2] P. L. Bartlett, D. J. Foster, and M. J. Telgarsky, “Spectrally-normalized margin bounds for neural networks,” in Advances in Neural Information Processing Systems 30, 2017.
[3] P. L. Bartlett, P. M. Long, G. Lugosi, and A. Tsigler, “Benign overfitting in linear regression,” arXiv preprint arXiv:1906.11300, 2019.
[4] M. Belkin, D. Hsu, S. Ma, and S. Mandal, “Reconciling modern machine learning practice and the bias-variance trade-off,” Proceedings of the National Academy of Sciences, vol. 116, no. 32, pp. 15849–15854, 2019.
[5] M. Belkin, D. Hsu, and P. Mitra, “Overfitting or perfect fitting? Risk bounds for classification and regression rules that interpolate,” in Advances in Neural Information Processing Systems 31, 2018, pp. 2306–2317.
[6] M. Belkin, D. Hsu, and J. Xu, “Two models of double descent for weak features,” arXiv preprint arXiv:1903.07571, 2019.
[7] M. Belkin, S. Ma, and S. Mandal, “To understand deep learning we need to understand kernel learning,” in International conference on machine learning, 2018, pp. 541–549.
[8] M. Belkin, A. Rakhlin, and A. B. Tsybakov, “Does data interpolation contradict statistical optimality?” in The Twenty-Second International Conference on Artificial Intelligence and Statistics, 2019, pp. 1611–1619.
[9] L. Breiman, “Reflections after refereeing papers for NIPS,” in The mathematics of generalization, D. Wolpert, Ed. 1995, pp. 11–15.
[10] L. Chizat, E. Oyallon, and F. Bach, “On lazy training in differentiable programming,” in Advances in Neural Information Processing Systems 32, 2019.
[11] T. Cover and P. Hart, “Nearest neighbor pattern classification,” IEEE Transactions on Information Theory, vol. 13, no. 1, pp. 21–27, 1967.
[12] L. Devroye, L. Györfi, and A. Krzyżak, “The Hilbert kernel regression estimate,” Journal of Multivariate Analysis, vol. 65, no. 2, pp. 209–227, 1998.
[13] E. Fix and J. L. Hodges, Jr., “Discriminatory analysis. Nonparametric discrimination: Consistency properties,” USAF School of Aviation Medicine, Randolph Field, TX, Project 21-49-004, Report 4, 1951.
[14] B. Ghorbani, S. Mei, T. Misiakiewicz, and A. Montanari, “Linearized two-layers neural networks in high dimension,” arXiv preprint arXiv:1904.12191, 2019.
[15] N. Golowich, A. Rakhlin, and O. Shamir, “Size-independent sample complexity of neural networks,” in Thirty-First Conference on Learning Theory, 2018, pp. 297–299.
[16] T. Hastie, A. Montanari, S. Rosset, and R. J. Tibshirani, “Surprises in high-dimensional ridgeless least squares interpolation,” arXiv preprint arXiv:1903.08560, 2019.
[17] T. Hastie, R. Tibshirani, and J. Friedman, The elements of statistical learning. Springer, 2001.
[18] H. He and W. J. Su, “The local elasticity of neural networks,” arXiv preprint arXiv:1910.06943, 2019.
[19] A. Jacot, F. Gabriel, and C. Hongler, “Neural tangent kernel: Convergence and generalization in neural networks,” in Advances in Neural Information Processing Systems 31, 2018, pp. 8571–8580.
[20] S. Lawrence, C. L. Giles, and A. C. Tsoi, “What size neural network gives optimal generalization? Convergence properties of backpropagation,” Institute for Advanced Computer Studies, University of Maryland, UMIACS-TR-96-22, 1996.
[21] T. Liang and A. Rakhlin, “Just interpolate: Kernel "ridgeless" regression can generalize,” arXiv preprint arXiv:1808.00387, 2018.
[22] S. Mei and A. Montanari, “The generalization error of random features regression: Precise asymptotics and double descent curve,” arXiv preprint arXiv:1908.05355, 2019.
[23] V. Muthukumar, K. Vodrahalli, and A. Sahai, “Harmless interpolation of noisy data in regression,” arXiv preprint arXiv:1903.09139, 2019.
[24] E. A. Nadaraya, “On estimating regression,” Theory of Probability & Its Applications, vol. 9, no. 1, pp. 141–142, 1964.
[25] P. Nakkiran, G. Kaplun, Y. Bansal, T. Yang, B. Barak, and I. Sutskever, “Deep double descent: Where bigger models and more data hurt,” arXiv preprint arXiv:1912.02292, 2019.
[26] B. Neyshabur, S. Bhojanapalli, and N. Srebro, “A PAC-Bayesian approach to spectrally-normalized margin bounds for neural networks,” in International Conference on Learning Representations, 2018.
[27] R. Salakhutdinov, “Tutorial on deep learning,” 2017. [Online]. Available: https://simons.berkeley.edu/talks/tutorial-deep-learning.
[28] R. E. Schapire, Y. Freund, P. L. Bartlett, and W. S. Lee, “Boosting the margin: A new explanation for the effectiveness of voting methods,” The Annals of Statistics, vol. 26, no. 5, pp. 1651–1686, 1998.
[29] D. Shepard, “A two-dimensional interpolation function for irregularly-spaced data,” in Proceedings of the Twenty-Third ACM National Conference, 1968.
[30] V. Vapnik, “Principles of risk minimization for learning theory,” in Advances in Neural Information Processing Systems 4, 1992.
[31] G. S. Watson, “Smooth regression analysis,” Sankhyā: The Indian Journal of Statistics, Series A, pp. 359–372, 1964.
[32] J. Xu and D. Hsu, “On the number of variables to use in principal component regression,” in Advances in Neural Information Processing Systems 32, 2019.
[33] G. Yehudai and O. Shamir, “On the power and limitations of random features for understanding neural networks,” in Advances in Neural Information Processing Systems 32, 2019.
[34] C. Zhang, S. Bengio, M. Hardt, B. Recht, and O. Vinyals, “Understanding deep learning requires rethinking generalization,” in International Conference on Learning Representations, 2017.
Related articles
- Letter from the Director, June 2020
- Computational and Statistical Tools to Control a Pandemic | Theoretically Speaking
- Berkeley in the 80s: Manuel Blum
- Simons Institute Polylogues: Algorithms and Race
- Differential Privacy: Issues for Policymakers
- From the Inside: The Quantum Wave in Computing
- From the Inside: Lattices: Algorithms, Complexity, and Cryptography
- Research Vignette: The Many Dimensions of High-Dimensional Expanders
- Cooks, in Theory


