Abstract
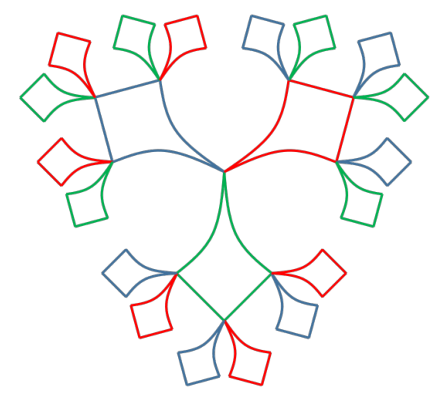
Let X be the infinite graph partially pictured below, the "free product graph" C_4 * C_4 * C_4. Let FinQuo(X) be the set of all finite graphs G that covered by X (i.e., that 'locally resemble' X; i.e., that consist of C_4's joined 3-to-a-vertex). A known Alon-Boppana-type theorem implies that every G in FinQuo(X) has second eigenvalue at least sqrt(5sqrt(5)+11) - o(1), where that magic number is the spectral radius of X. We may then ask the "Ramanujan question": are there infinitely many G in FinQuo(X) with second eigenvalue at most sqrt(5sqrt(5)+11)? When X is the infinite d-regular tree, this is the well known Ramanujan graph problem resolved by Marcus, Spielman, and Srivastava [MSS].
We show a positive answer to the problem for a wide variety of infinite X (not necessarily trees). Techniques involve a new infinite graph product, a new graph polynomial (generalizing the matching polynomial), "freelike walks", Heaps of Pieces, and of course [MSS]'s Interlacing Polynomials Method.
Joint work with Sidhanth Mohanty (CMU/Berkeley).