Research Vignette: Setting Posted Prices Under Uncertainty

by Amos Fiat, Tel Aviv University
Selfish Behaviour and Uncertainty
The author had the undeserved great fortune to be invited to two semesters at the Simons Institute for the Theory of Computing. The author had a truly wondrous time and is immensely grateful for the this fantastic opportunity. The opportunity to hear and interact with the amazing people attending was priceless. Thus, when asked to write a short Research Vignette,1 the author felt that it would be churlish to object strenuously. One can but hope that this is not yet another example of an error in judgment.2
Aspects of uncertainty have been studied in many disciplines, including philosophy, psychology, physics, the life sciences, economics and computer science, among others. In this Vignette, we address some aspects and models of uncertainty in statistics, computer science, and economics.
Temporal uncertainty occurs where the future or certain aspects of the future are unknown. Decisions made today (e.g., agreeing to write this article) may have unforseen consequences tomorrow (when the disastrous NYT critique is published). Optimal stopping theory,3 prophet inequality settings,4 secretary settings,5 and competitive analysis of online algorithms6 all deal with aspects of and models for temporal uncertainty. This vast body of work includes both Bayesian and worst-case models.
Another element of uncertainty arises when selfish agents interact. Clearly, it is useful to know how much a customer is willing to pay before trying to sell her something. Given that the techniques used by Torquemada are often condemned,7 one needs to be more subtle when considering the impact of private information.
One approach is to consider rational behavior and study resulting equilibria.8 Pricing equilibria (competitive equilibria) have been studied in many settings.9 Social choice theory10 and mechanism design11 seek to engineer algorithms so as to achieve certain desired goals. A wide variety of equilibrium notions have been defined, including dominant strategy, Bayes-Nash, and many others.
The computer science outlook is to quantify things – in this case, how good an outcome arises in equilibria when compared to optimal outcomes,12 and what mechanisms can be implemented in poly time.13
The setting of interest
Consider a model of online decision-making mechanisms in which selfish agents arrive sequentially, and the mechanism decides upon an outcome and payment for each arriving agent, where payments are used to align the incentives of the agent with that of the mechanism. There is temporal uncertainty because the preferences of the agents (their types) are unknown. The agent may have an opportunity to specify her type, but the decisions made by the mechanism might not be in the best interest of the agent. This may result in the agent strategically misrepresenting her preferences so as to achieve a better outcome for herself. A mechanism is truthful if it is always in the best interest of the agent to report her type truthfully.
For some time I have been obsessed with a specific class of truthful online mechanisms that take the form of dynamic posted prices.14 The assumption here is that the future is entirely unknown, and can be determined adversarially with no guarantees on future behavior. Dynamic pricing schemes are truthful online mechanisms that post prices for every possible outcome, before the next agent arrives. Then, the agent chooses the preferred outcome — minimizing the cost for the outcome plus the price tag associated with the outcome.
Online problems are either minimization problems (e.g., minimize the sum of costs) or maximization problems (e.g., maximize the number of agents served). Although optimal solutions to maximization/minimization objectives can be cast as the other, the competitive ratio is quite different in the two settings. Online algorithms have been devised with both maximization and minimization objectives. The technique of "classify and randomly select" often gives simple randomized algorithms for maximization objectives which also naturally translate into truthful mechanisms. In contrast, minimization objectives (e.g., k-server and makespan) require entirely different techniques. Converting online algorithms into mechanisms without performance degradation opens up an entire new class of problems for which incentive compatible mechanism design is applicable.
We note there are many other problems where posted prices play a major role, within widely differing models, information states, and various stochastic assumptions.15
A dynamic pricing scheme is inherently truthful, since prices are determined irrespective of the type of the next agent. Posted price mechanisms have many additional advantages over arbitrary truthful online mechanisms. In particular, such mechanisms are simple: agents need not trust or understand the logic underlying the truthful mechanism, agents are not required to reveal their type, and there is no need to verify that the agents follow the decision made by the truthful online mechanism.
A posted price mechanism is a truthful online algorithm, and as such, can perform no better than the best online algorithm. The main goal of this approach is to study the performance of dynamic posted price mechanisms (quantified by the competitive ratio measure) and compare them with the performance of the best online algorithm. One may think of this problem as analogous to one of the central questions in algorithmic mechanism design in offline settings: compare the performance of the best truthful mechanism (quantified by the approximation ratio measure) with the performance of the best non-truthful algorithm.
In a paper at EC 2017, Feldman, Roytman and I presented constant competitive dynamic pricing schemes for makespan minimization in job scheduling. Events represent jobs; the job type contains the job’s processing times on various machines. Agents seek to complete their job as soon as possible, and therefore prefer to be assigned to a machine whose load (including the new job) is minimized.16 One can consider so-called related machines (where machines have speeds, and jobs have some quantity of work to be done) and unrelated machines (where the time associated with a job arbitrarily depends on the machine). Previous online algorithms for the problem17 are not truthful — in that a job may misrepresent its size so as to get a preferential assignment to a machine.
An online truthful mechanism for this setting determines an allocation and payment for each arriving agent upon arrival. That is, upon the arrival of a job, based on the job’s processing times, the mechanism assigns the job to some machine and determines the payment the agent should make. The cost of an agent is the sum of the machine’s load (including her own processing time) and the payment. Each agent seeks to minimize her cost.
A dynamic posted price mechanism for this setting sets prices on each machine, before the next agent arrives (prices may change over time). The next agent to arrive seeks to minimize her cost, i.e., the load on the chosen machine (including her own load) plus the posted price on the machine. The agent breaks ties arbitrarily.
An example of dynamic pricing: Makespan minimization, related machines
We now motivate how dynamic pricing is useful, via a small example. We do so by comparing the schedule produced without any pricing to the schedule produced via a dynamic pricing scheme. Schedules obtained without pricing are equivalent to schedules produced by the greedy algorithm that assigns each job j to a machine i that minimizes ℓi(j − 1) + (the load on machine i prior to the arrival of job j, plus the additional time required for job j itself).
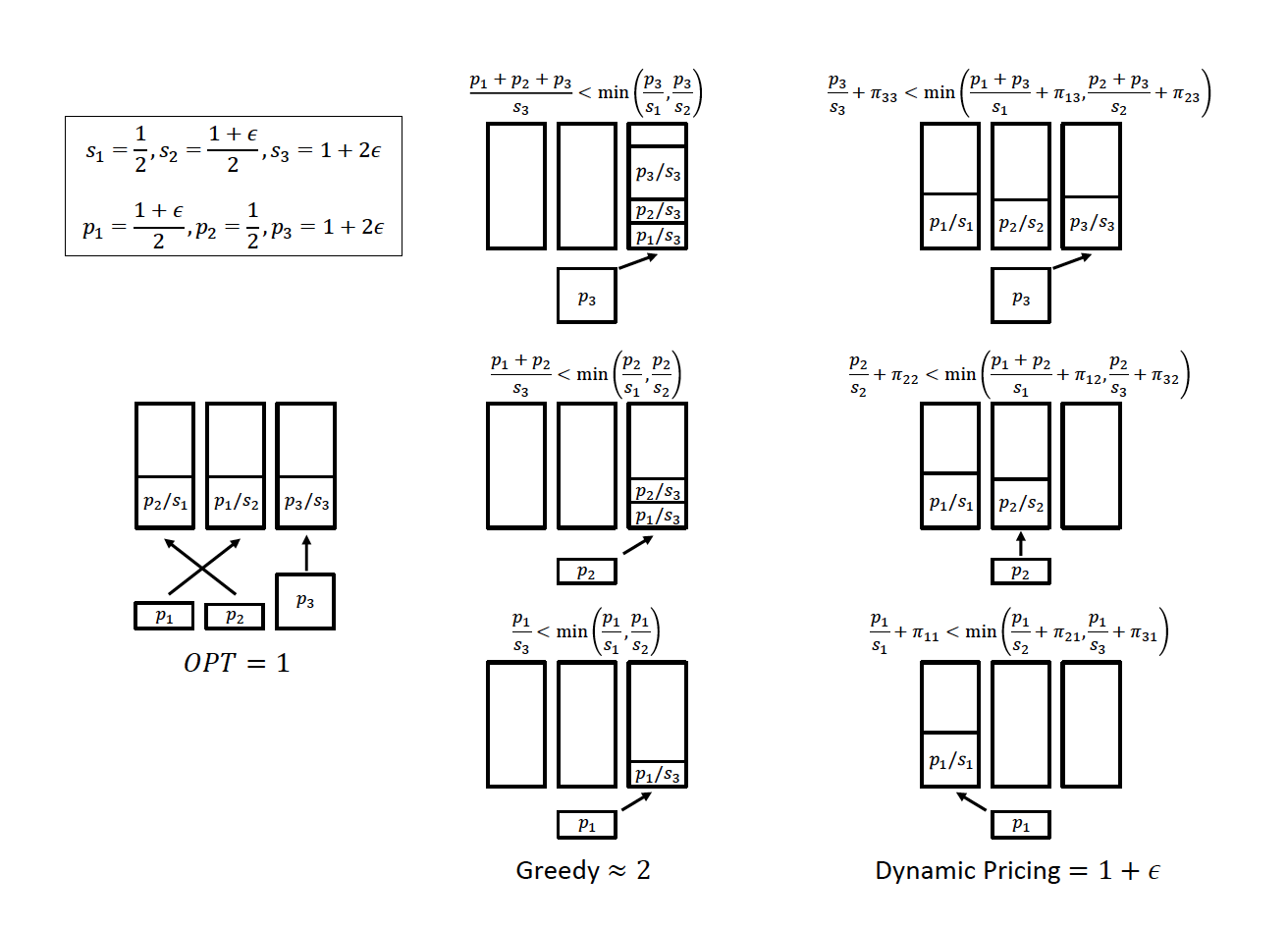
Figure 1: Related machines: the optimal makespan, the greedy algorithm, and dynamic pricing. The algorithm for setting dynamic prices is missing.
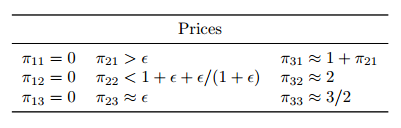
In our example (given as Figure 1) there are m = 3 machines, with speeds s1 = , s2 = (1 + ϵ), and s3 = 1 + 2ϵ; and n = 3 jobs, with sizes p1 = (1 + ϵ), p2 = , and p3 = 1 + 2ϵ. The left, middle, and right columns show the optimal assignment, the greedy assignment, and the assignment obtained by our dynamic pricing scheme, respectively. In the middle and right columns, the arrival order is from bottom to top.
Optimal makespan: The optimal makespan is L∗ = 1, achieved by assigning job 1 to machine 2, job 2 to machine 1, and job 3 to machine 3.
Greedy: The greedy algorithm assigns job 1 to machine 3, since the machine i that minimizes is the fastest machine (initially, all loads are 0). Job 2 is also assigned to machine 3, since ℓ3(1) + = < = < (for sufficiently small ϵ > 0). Lastly, job 3 is also assigned to machine 3, since ℓ3(2) + = < = < . Hence, the greedy algorithm assigns all jobs to machine 3, resulting in a makespan of ≈ 2.
Pricing scheme: Our dynamic pricing scheme sets prices before the arrival of each job, which are independent of the type of the incoming job. We omit the explanation as to how to set these prices.18 The important aspect is that these prices are set before knowing what the next job will be. The performance guarantee must hold irrespective of the future. Let cij be the cost of job j on machine i; this is the sum of the completion time and the additional posted price currently on the machine.
Job 1 chooses machine 1, since c11 = + π11 = 1 + ϵ < 1 + π21 = + π21 = c21 < + 1 + π21 ≈ + π31 = c31.
Prior to the arrival of job 2, the dynamic pricing scheme sets new prices (see Figure 1), and job 2 chooses machine 2, since c22 = + π22 < + 1 + ϵ + = ℓ1(1) + = c12 < + 2 ≈ + π32 = c32.
Finally, prior to the arrival of job 3, the dynamic pricing scheme sets yet new prices and job 3 chooses machine 3, since c33 = + π33 ≈, while c13 = ℓ1(2) + = 1 + ϵ + 2p3 ≈ 3 and c23 = ℓ2(2) + + π23 = + + π23 ≈ 3.
Since machine 1 has the highest load, the schedule produced by our dynamic pricing scheme achieves a makespan of ℓ1(3) = 1 + ϵ. This example can be extended to show that greedy can be as bad as Ω(log m)-competitive, while in contrast our dynamic pricing scheme is O(1)-competitive.
During a talk in the Fall 2017 Simons Institute program on Algorithms and Uncertainty, I proposed that one study dynamic pricing schemes for flow time; and indeed, one definite outcome of this semester is a paper by Im, Moseley, Pruhs and Stein that comes up with a constant competitive dynamic pricing scheme to minimize the maximum flow time (the maximum time an agent is in the system). This improves on the previous online algorithm for the problem in terms of the competitive ratio, and has the added advantage of being truthful and simple.
Online algorithms, online mechanisms, and dynamic pricing
One critical question is the following: where do the boundaries lie between online algorithms, online mechanisms (not dynamic pricing) and dynamic pricing? In our EC paper, we show that there exist problems – makespan minimization on unrelated machines, where the pair (job, machine) determines the processing time – where good online mechanisms exist but there are no good dyanmic pricing schemes.
The connection between online mechanisms and dynamic pricing schemes is not entirely trivial.19 Dynamic pricing schemes are obviously truthful mechanisms, but converting an arbitrary online mechanism into a dynamic pricing scheme may not be possible.
We can show that online mechanisms with certain performance guarantees that also have properties a to c below can be converted into dynamic pricing schemes with the same guarantee: a) the online mechanism must be prompt (where the payments are determined immediately); b) ties in agent utilities do not arise, or can be resolved arbitrarily without harming performance guarantees — this is not an issue in the mechanism-design setting because the mechanism may decide how to break ties, but it is an issue with pricing schemes; and c) the mechanism does not require "voluntary revelation" of agent types – in pricing schemes, the only information available to the dynamic pricing scheme is what the previous agents actually chose; pricing schemes are not direct revelation schemes.
Afterword
It has been a pleasure discussing these and other problems with researchers visiting the Simons Institute, and at my home site, Tel Aviv University. I am grateful for discussions with and gracious instruction from Nikhil Bansal, Avrim Blum, Alon Eden, Michal Feldman, Anupam Gupta, Ilia Gorlick, Haim Kaplan, Anna Karlin, Dick Karp, Thomas Kesselheim, Bobby Kleinberg, Elias Koutsoupias, Stefano Leonardi, Christos Papadimitriou, Kirk Pruhs, Tim Roughgarden, and Matt Weinberg. In various combinations, we have tried to attack many other online problems via dynamic pricing. Many of these are wide open; some (minor) progress has been made on others. Many an idea arose in the numerous talks and discussions at the Simons Institute.
Notes
1Merriam-Webster online dictionary: 2a) a short descriptive literary sketch; 2b) a brief incident or scene (as in a play or movie).
2According to Aristole (Poetics, 4rd century BCE), an ideal tragedy is caused by error in judgment by the protagonist, and not by unavoidable error.
3Wald (1945), Arrow, Blackwell and Girshick (1948); Snell (1952).
4Cayley (1875); Krengel, Sucheston and Garling (1977).
5Kepler (1613); Martin Gardner (1960); Gibert and Mosteler (1966).
6Sleator and Tarjan (1985).
7Recent political developments in North America notwithstanding.
8von Neumann (1928).
9Cournot (1838); Walras (1874); Arrow and Debreu (1954).
10Condorcet (1785); Arrow (1951); Gibbard and Satterthwaite (1973,1975).
11Hurwicz, Maskin and Myerson (2007).
12Koutsoupias and Papadimitriou (1999).
13Nisan and Ronen (1999).
14Fiat, Mansour and Nadav (2008) — Packet routing; Cohen-Addad, Eden, Fiat and Jeż (2015) — Task systems, k-server, and metrical matching; Feldman, Fiat and Roytman (2017) — Makespan minimization; Im, Moseley, Pruhs and Stein (2017), the latter two discussed herein.
15E.g., Myerson’s virtual values, prophet inequalities, secretary problems, combinatorial markets – Feldman, Gavin and Lucier (2013, 2015 and 2016); Envy-free pricings – Guruswami, Hartline, Karlin, Kempe, Kenyon and McSherry (2005); and many others.
16In this interpretation, "load" is the time required by the server to deal with all current jobs in the server queue, and jobs are processed in a first-in, first-out manner, i.e., jobs enter a server queue.
17Awerbuch, Azar, Fiat, Plotkin and Waarts (1993).
18EC17 and on the archive.
19Many thanks to Moshe Babaioff, Liad Blumrosen, Yannai A. Gonczarowski and Noam Nisan for discussions helpful in clarifying this point.
Related Articles
- Letter from the Director, Summer 2017
- Machine Learning Becomes the New “Plastics,” Transforming the Once-Isolated World of CS Theory
- From the Inside: Foundations of Machine Learning
- From the Inside: Pseudorandomness
- Research Vignette: Entangled Solutions to Logic Puzzles
- Looking Ahead: Bridging Continuous and Discrete Optimization





