Research Vignette: Quantum PCP Conjectures

By Thomas Vidick

The macroscopic properties of materials arise from the physical interactions between their constituent particles. For example, the use of the Pauli exclusion principle explains how the conductivity properties of a material follow from the energy band structure of its atoms. Techniques for performing the extrapolation from microscopic laws to macroscopic predictions form the basis of statistical mechanics. The implied statistical averaging, however, is insufficient to predict certain properties, such as superconductivity, for which subtle quantum mechanical effects need to be taken into account. Without the reduction in complexity granted by the application of the law of large numbers, the study of novel phases of matter quickly runs into a fundamental computational bottleneck. The complete description of an n-particle quantum system requires exponentially many parameters: How can one hope to make meaningful predictions if one cannot even write down a full description of the state of the system? Is materials science about to hit a computational barrier?

The Simons semester on Quantum Hamiltonian Complexity brought together theoretical physicists and computer scientists motivated by this problem. The goal of the semester was to formulate, and begin to address, the key complexity-theoretic issues that arise from the study of many-body systems in condensed-matter physics. A central conjecture, the so-called quantum PCP conjecture, crystallizes many of these issues, and the conjecture was hotly debated throughout the semester. During an open problems session held as part of one of the week-long workshops, I was prompted to formulate a new variant of the conjecture whose study led to a fruitful collaboration with Joseph Fitzsimons, another program participant. Before describing this new variant, I will introduce the central computational problem in quantum Hamiltonian complexity and formulate the quantum PCP conjecture.

The local Hamiltonian problem

The computational hardness of making predictions about the global properties of quantum many-body systems is embodied in a single computational problem, the local Hamiltonian problem. This problem, introduced by Kitaev as a direct quantum analogue of classical constraint satisfaction problems, asks whether a given Hamiltonian (i.e., a collection of physical constraints—magnetic field, two-body interactions, etc.) acting on n particles has a lowest-energy state whose energy is below or above a certain threshold. Formally, each constraint is specified by a a positive semidefinite matrix H_j acting on a constant-size subset of the n particles. The energy of a quantum state |ψ〉 is its overlap with the total Hamiltonian:

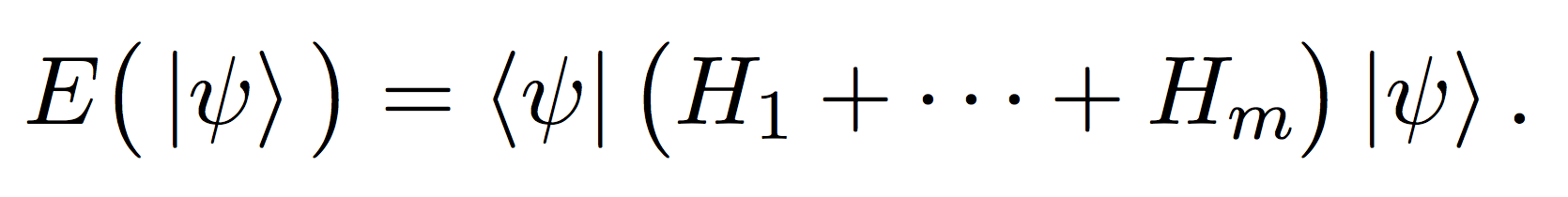
Kitaev showed that the local Hamiltonian problem is complete for the complexity class QMA, the quantum analogue of NP: QMA is the class of decision problems that can be solved by a polynomial-time quantum computer given access to a quantum proof. Kitaev's seminal result shows that a fundamental problem in physics, estimating the minimal energy of a local Hamiltonian, is computationally intractable. Assuming, as is widely believed, that QMA is a strictly larger class than NP, it also implies that the lowest-energy state does not have an efficient classical description from which its energy can be estimated. In particular, the state must be highly entangled; in other words it must possess complex quantum correlations spread across all its particles. Kitaev's purely theoretical result thus has direct consequences for the properties of physical states: even the simplest such states (the lowest-energy state is the equilibrium state of the system as the temperature is driven to zero) display the most complex quantum phenomenon, many-body entanglement.

The quantum PCP conjecture

Kitaev's hardness result applies to inverse-polynomial approximations to the minimal energy. What about weaker approximations? In cases where the energy has an intensive scaling with the system size it is natural to only require an approximation that is proportional to the number of constraints acting on the system. Do such approximations remain hard to obtain, or could they be amenable to efficient, possibly quantum, algorithms?

Asking this question amounts to seeking a quantum analogue of the PCP theorem from classical complexity theory. The PCP theorem, a major breakthrough of the early 90s, asserts that constraint satisfaction problems such as 3SAT remain hard even under very strong promises on the satisfiability of the instance: Given a 3SAT formula, it is NP-hard to estimate the maximum number of clauses that can be simultaneously satisfied up to an accuracy that scales proportionally with the total number of constraints. Since the local Hamiltonian problem contains classical constraint satisfaction problems as a special case, the PCP theorem implies that constant-factor approximations to the minimal energy are NP-hard. The quantum PCP conjecture asks whether the problem is even harder: Could it be QMA-hard?

The status of the conjecture remains completely open. A positive answer would have important implications for the presence of entanglement in so-called Gibbs states, which are equilibrium states of the Hamiltonian at low but positive temperature. Indeed, interest in the conjecture partly stems from its apparent contradiction with the common physical intuition that, as temperature is increased above zero, disorder in the system tends to destroy the coherence required for maintaining entanglement. If this intuition were correct, then low-energy states would have classical descriptions that could be used to contradict the conjecture.

A new variant

Much of the strength of the PCP theorem comes from its versatility, and many equivalent formulations are known. One such formulation, closely tied to the theorem's origins, uses the language of interactive proof systems. Here one thinks of the verification procedure (for, say, the satisfiability of a 3SAT formula given as input) as an interactive protocol between a polynomial-time verifier and all-powerful but untrusted provers. The PCP theorem implies that any language in NP can be verified through a single round of interaction with two non-communicating provers, to which the verifier sends logarithmic-length messages and receives a constant number of bits as answers. The possibility for such highly efficient proof checking (compared to reading off the linear number of bits describing a satisfying assignment) remains a wonder of modern complexity theory.

Interestingly, this formulation of the PCP theorem gives rise to a quantum analogue whose relation to the quantum PCP conjecture is a priori unclear. The new variant asks the following: Do all languages in QMA admit an efficient verification procedure of the above form, in which the verifier and communication may be quantum? Here it is important to also allow the provers to be initialized in an arbitrary entangled state, as this may be necessary to encode the QMA witness whose existence the provers are supposed to convey to the verifier.

Prompted by program participants Dorit Aharonov and Umesh Vazirani, I formulated this new variant, and the question of its relation to the traditional quantum PCP conjecture, during an open problems session that we had organized as part of the first workshop of the semester. The question immediately generated many ideas and suggestions from the audience. The problem is a tantalizing one. How can the existence of a global, n-qubit state be verified solely through the local snapshots obtained by the verifier in the interactive proof system? In the classical setting, consistency between the provers' answers and a global proof is ensured by cross-checking the provers' answers against each other through a complexity-theoretic implementation of the classic prisoner's dilemma interrogation technique. In the case of a quantum proof, however, the presence of entanglement renders such cross-checking all but impossible, as the no-cloning principle prevents even honest provers from sharing "consistent" copies of the same quantum state; with a unique copy, the question of who owns which part of the proof becomes essential.

Joseph Fitzsimons, a participant from the Centre for Quantum Technologies in Singapore, suggested a scheme based on encoding the quantum proof using secret-sharing, and distributing the shares equally among the provers. I was excited by his idea, and we attempted to flesh out the details during the semester, continuing by Skype after Joe had left for Singapore. We were recently able to complete the soundness analysis of Joe's suggested protocol, and our findings establish the second variant of the quantum PCP conjecture as a promising target for future work. Extending the naïve scheme that we have so far been able to analyze in order to obtain a protocol with better soundness guarantees is an exciting open problem. I expect its resolution to require the development of quantum codes with new properties, akin to the locally testable codes used in proofs of the PCP theorem, but possibly with an even more local twist. This would be an exciting outcome, independently of the eventual validity of the conjecture.

These explorations were made possible by the diverse mix of participants in the semester and their willingness to engage with one another. As I was stating my question in the open problems session, encouraged to do so by other participants, I more or less firmly believed that it could only lead to a dead end—but this did not take into account the generous creativity of my fellow participants!

Related Articles:

Letter from the Director
Profile of Luca Trevisan, the Simons Institute's Incoming Senior Scientist
From the Inside: Algorithmic Spectral Graph Theory
From the Inside: Algorithms and Complexity in Algebraic Geometry
Research Vignette: On Sex, Math, and the Origin of Life