Research Vignette: Semialgebraic Geometry of Ranks

By Kaie Kubjas
The rank of a matrix M is a fundamental notion in linear algebra. While usually defined as the dimension of the span of the rows or the span of the columns, it could also be defined as the minimal number r such that the matrix M admits a factorization as M=AB, where A has r columns and B has r rows. If all entries of the matrix M are nonnegative, then such a factorization can be pictured as a pair of nested polytopes: the outer one is given by the inequalities Ax≥0, and the inner one by the convex hull of the columns of B. Up to an affine transformation, this picture is independent of the specific factorization AB.
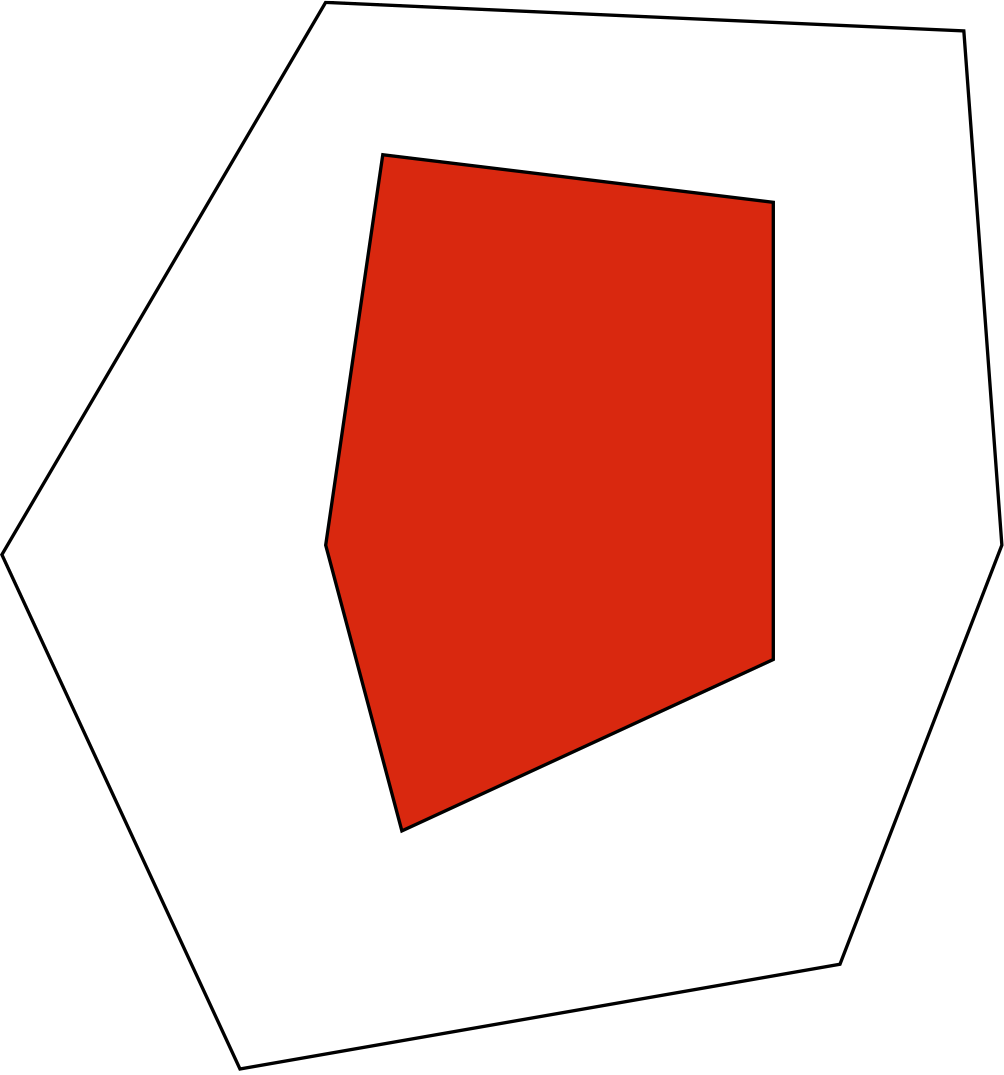 Figure 1: Two nested polygons corresponding to a rank 3 matrix with 6 rows and 5 columns
Figure 1: Two nested polygons corresponding to a rank 3 matrix with 6 rows and 5 columns
In many applications, we are interested in factorizations of a certain particular form. For example, we can study factorizations M=AB where A,B have nonnegative entries. The minimal r as above for which such a factorization exists is called the nonnegative rank. Cohen and Rothblum formulated this definition geometrically: a nonnegative matrix M has nonnegative rank at most r if and only if there exists a polytope with r vertices that can be fitted between two nested polytopes associated with the matrix.
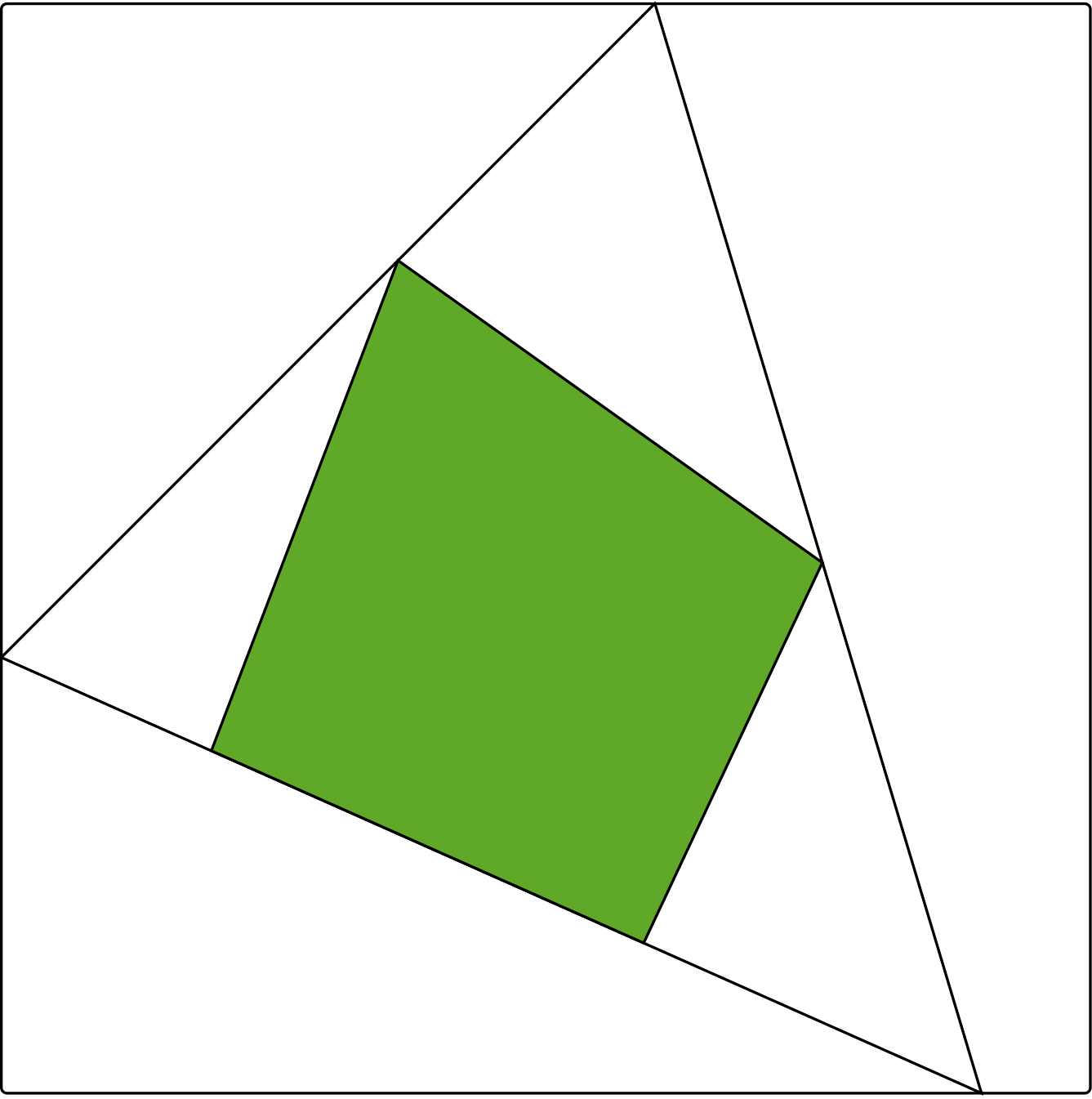 Figure 2: Two quadrangles and a triangle between them
Figure 2: Two quadrangles and a triangle between them
The interest in the nonnegative rank started in the combinatorial optimization community with the work of Yannakakis at the end of the 1980s. A linear program aims to minimize or maximize a linear function over a region that is given by linear constraints, i.e., a polyhedron or a polytope. Yannakakis showed that the minimal number of variables and constraints needed to express a linear program over a polytope is closely related to the nonnegative rank of a matrix associated to this polytope.
One line of research that started with the seminal paper of Yannakakis studies lower bounds on the nonnegative rank, and later also on the positive semidefinite rank, for different polytopes that appear in combinatorial optimization. For example, the Traveling Salesman Problem (TSP) asks: Given a list of cities, what is the shortest cycle that visits every city exactly once? It can be formulated as a linear program over a region which is called the TSP polytope. The TSP problem is NP-hard, and some of the attempts to prove P=NP aimed to give polynomial formulations of the TSP polytope. This motivated Yannakakis to look for superpolynomial lower bounds on the nonnegative rank of the TSP polytope, which was completed by Fiorini et al. in 2012.
The notion of nonnegative rank also appears in statistics: The set of stochastic matrices of nonnegative rank at most r is called the r-th mixture model. It represents the joint probabilities of two random variables that are independent given a third random variable with r possible values. Given a data matrix that is obtained by an opinion poll or a measurement, one would like to estimate the parameters of the true probability distribution that the data come from. Specifically, the maximum likelihood estimate of a data matrix is a matrix in the r-th mixture model that maximizes a specific function, called the likelihood function. There are several ways for numerically solving the maximum likelihood estimation in practice. These methods, however, do not provide a certificate for having found the global optimum.
In my recent research together with Eggermont, Horobeţ, Robeva, and Sturmfels (Robeva and Sturmfels attended the Algebraic Geometry program, and Horobeţ participated in one of the workshops at the Simons Insitute), we have been interested in exact descriptions of the sets of matrices of nonnegative rank at most r. They are semialgebraic sets, which means that they can be characterized by Boolean combinations of polynomial equations and inequalities. Knowing quantifier-free semialgebraic descriptions of these sets would give an exact method for checking if a matrix lies in them. It would be also an essential step towards computing maximum likelihood estimates with certificate.
We begin by studying the matrices of non-negative rank at most three. Recall that in geometric terms, a matrix has nonnegative rank at most three if and only if one can fit a triangle between two polygons that are associated with the matrix, as in Figure 2. Together with Robeva and Sturmfels, we designed a very simple algorithm for checking whether this can be done. One needs to check only one triangle for every vertex of the outer polygon and one triangle for every edge of the inner polygon. The main importance of this simple algorithm is that it can be turned into a semialgebraic description for the set of matrices of nonnegative rank at most three.
Using this algorithm, we have been able to answer a question by Cohen and Rothblum in the first nontrivial case: We show that if a matrix of nonnegative rank 3 has rational entries, then it admits a factorization as above where A and B have rational entries. This is the first progress on this question in 20 years. It remains unsolved whether this is true for higher nonnegative rank.
One aim for the future is to develop an algorithm for checking higher nonnegative rank that could be turned into an exact semialgebraic description and/or that would give an insight to the question of Cohen and Rothblum. The difficulty lies in studying higher dimensional nested polytopes, in which case much less is known than about nested polygons.
Another generalization of the regular rank is the positive semidefinite (psd) rank. Formally, the psd rank of a nonnegative matrix M is the smallest natural number k such that M can be factored as AB, where rows of A and columns of B are entries of k×k psd matrices written in vectorized form. Or, geometrically: a nonnegative matrix M has psd rank at most k if and only if there exists an affine slice of the cone of k×k psd matrices, also known as a spectrahedron, that can be fitted in between two nested polytopes associated with the matrix.
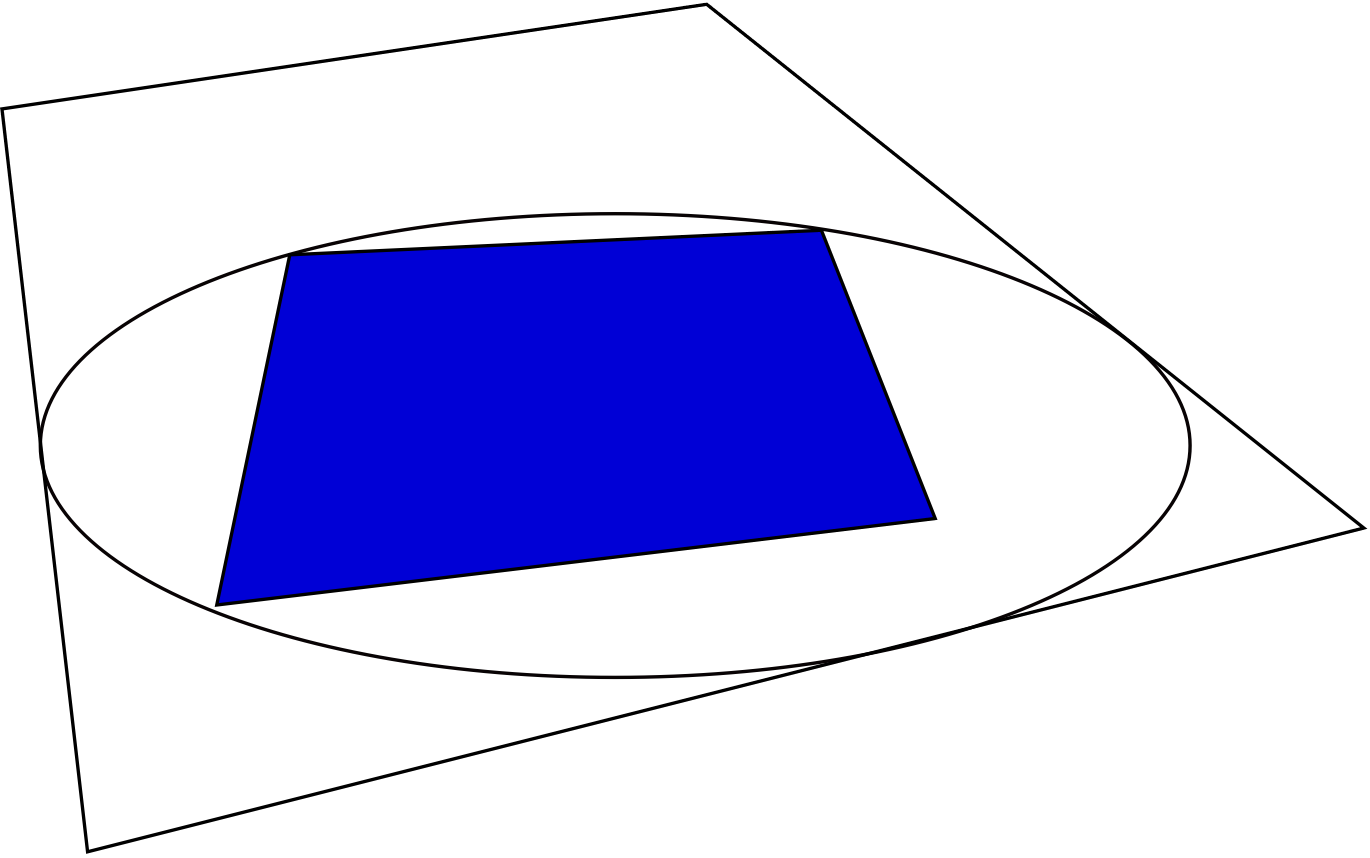 Figure 3: Two quadrangles and an ellipse between them
Figure 3: Two quadrangles and an ellipse between them
Psd rank was one of the topics that was common to both programs in Fall 2014: Lee, Raghavendra and Steurer, who were participants in the concurrent Spectral Graph Theory program, have recently proved superpolynomial lower bounds on the psd rank of several families of polytopes appearing in combinatorial optimization, extending the work on nonnegative rank. Parrilo, who was a participant in both the Algebraic Geometry program and the Spectral Graph Theory program, is one of the founders of the theory of psd rank.
Together with Robeva and Robinson, we have studied the set of matrices of rank three and psd rank two. In this case, the slice of the cone of 2×2 psd matrices is an ellipse. It turns out that unless the ellipse between two polygons touches the outer polygon at three points and goes through three vertices of the inner polygon, one can always perturb the polygons by a little, and still find an ellipse fitted between them. Hence having an ellipse between the polygons that touches both of them at three points is a necessary condition for being on the boundary of the semialgebraic set of matrices of rank at most three and psd rank at most two. This geometric condition can be translated to a polynomial equation, which defines the closure of a boundary of this set.
The aims for the future are to translate these boundary components to a semialgebraic description and to understand the geometry of matrices of higher psd rank. Again, as in the nonnegative rank case, this requires studying higher dimensional polytopes and general spectrahedra fitted between them.
For further reading:
K. Kubjas, E. Robeva, and B. Sturmfels: Fixed points of the EM algorithm and nonnegative rank boundaries. Annals of Statistics, 43(1), 422–461, 2015.
J. R. Lee, P. Raghavendra and D. Steurer: Lower bounds on the size of semidefinite programming relaxations. STOC 2015.
Related Articles:
Letter from the Director
Through the Computational Lens: Interdisciplinary Collaboration at the Simons Institute
From the Inside: Information Theory
Research Vignette: Faster Algorithms for Linear Programming
Program Preview: Cryptography


